4カード問題(ウェイソン選択課題)というものをご存知でしょうか。
4枚のカードの表裏がどうなっているのかを確かめるという問題であり、よく考えれば簡単に分かる内容なのですが、なぜか間違えてしまう人が多いことで有名な問題です。
今回はそんな4カード問題とは何かについて、わかりやすく簡単に解説していこうと思います。
4カード問題(ウェイソン選択課題)とは
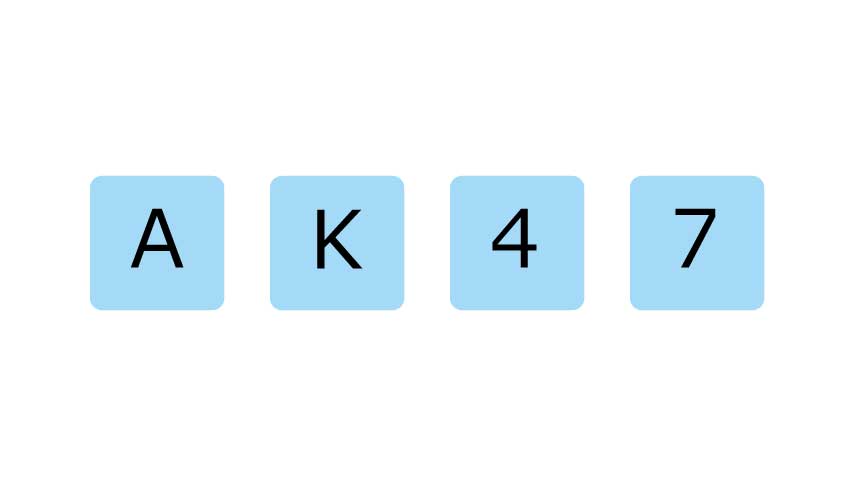
A、K、4、7の4枚のカードがあります。アルファベットの裏には数字、数字の裏にはアルファベットが書かれています。
「片面が母音ならばそのカードの裏面は偶数でなければならない」
ということを確かめるためには、どのカードを裏返す必要があるでしょうか。
裏返す必要があるカードをすべて選びなさい。
これが4カード問題の具体例です。
A, K, 4, 7 である必要はないのですが、一番よく見られる例であると思います。
初めてこの問題を知ったという方は答えを見る前に一度考えてみてください。
答えは「A」と「7」です。
あなたの答えは正解でしたか?
よくよく考えたら「A」と「7」が答えだと分かるのですが、「A」と「4」が答えだと勘違いする人が多いようです。
一体なぜ、「A」と「4」だと間違えてしまうのでしょう?
4カード問題(ウェイソン選択課題)の解説
どうして「A」と「7」が答えなのでしょうか?
まずは考え方の解説をします。
問題文を読むと
「片面が母音ならばそのカードの裏面は偶数でなければならない」
と書いてあります。
「A」は母音であり裏が偶数であるかどうかを確かめる必要があるので「A」が答えだと分かるのですが、「偶数の裏は母音である必要はない」ため「4」の裏を確かめる必要はありません。
「4」の裏が母音でも子音でも問題ないということです。
しかし、「7」の裏が母音であった場合「片面が母音ならばそのカードの裏面は偶数でなければならない」というルールに違反してしまうため、「7」の裏を確かめる必要があります。
従って、答えは「A」と「7」になるというわけですね。
4カード問題の正答率
この問題は分かりにくい問題ですよね。ウェイソンの論文(国立国会図書館リサーチ ISBN 0521217563)によると正答率は10%未満であったとのことです。
この問題を間違えてしまう人の方が圧倒的に多いということであり、初見でこれを見ると「A」「4」と答えてしまう気持ちが分かります。
 かいしー
かいしー
4カード問題と飲酒



こう思った方は多いのではないでしょうか?
ここで、4カード問題の内容を飲酒(社会関係)に変えて問題を考えてみましょう。


ビール、お茶、35歳、16歳の4枚のカードがあります。飲み物の裏には年齢、年齢の裏に飲み物が書かれています。
「片面がアルコールならばそのカードの裏面は20歳以上でなければならない」
ということを確かめるためには、どのカードを裏返す必要があるでしょうか。
裏返す必要があるカードをすべて選びなさい。
4カード問題を飲酒に関連して考えてみたら答えが「ビール」と「16歳」だと一瞬で理解することができると思います。
問題の解説も必要ないですよね。
実際、こちらの問題の正答率は約73%もあります。
論理的な部分は数字とアルファベットのときと同じはずなのに、アルコールと年齢で考えると物凄く理解しやすくなる問題へと変化するのです。
4カード問題と心理学
人は論理だけで物事を考えているわけではありません。
日常の中にある具体的な知識を用いて物事を考えています。
このとき、ただ具体化すればいいというわけではありません。
日常的に使っていること=長期記憶を用いることで、物事は比較的に分かりやすくなります。
この4カード問題でも日常にあまり関わりのない具体的な事柄で例えてしまうと分かりにくくなってしまいます。
お酒と年齢というのは日常に私たちの深い関わりがあることなので、とても分かりやすくなっているということです。
日常生活に関係すると分かりやすくなる具体例
例えば、この数字を覚えてみてください
4960 1378 2947
はい、無理ですね。覚えられません。意味不明ですもん。頑張れば覚えられるかもしれませんが、明日には忘れています。
では、この数字ならどうでしょうか
1192 9876 2020
この数字は先程の数字と違い、数字の並びに法則があります。
いい国、9876、2020年…覚えやすいですよね。
何も法則のないように見える数字は覚えにくいですが、具体的な法則や長期記憶として残っているものならば覚えやすいです。
このように、説明をするときは日常的に関わりのある具体的な例えをすると良いと言えるでしょうね。
参考文献
今回参考にさせていただいた本です。
4カード問題だけではなく、オペラント条件づけ・パターン認知・プロスペクト理論・二重課題法など、かなりの量の心理学の実験についての内容がまとまっている一冊です。