・気体分子運動論とは
・気体分子運動論の結論
・球形容器の場合の気体分子運動論
今までは気体を巨視的(マクロ)な視点から考えていました。今回は、気体の分子一つ一つを見るようなとても細かい視点、つまり、ミクロな視点で考えていきます。
今回は、気体分子運動論の内容について、わかりやすく簡単に解説していきます。
気体分子運動論とは
分子の動きから気体の運動を考える理論
一辺の長さがLの立方体(体積V=L3)の中に質量mの単原子分子がN個あるとします。また、この気体は理想気体とします。
気体分子運動論では単原子分子理想気体を考えるという前提が、今後の問題を解くうえで大切なポイントとなります。
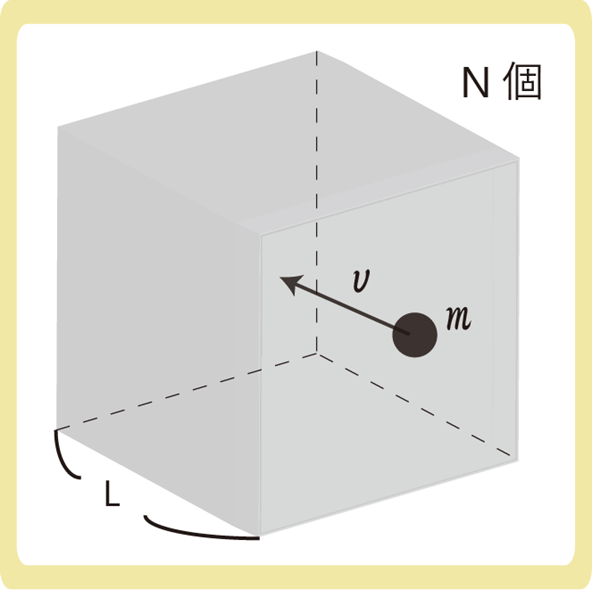
速さvで分子が運動しているとすると、分子の動きは3次元的な動きであるため、速さをxyzの3方向に分解し、\(v^2=v_x^2+ v_y^2+ v_z^2\)と式を作ることができます。
x方向のみを考えましょう。
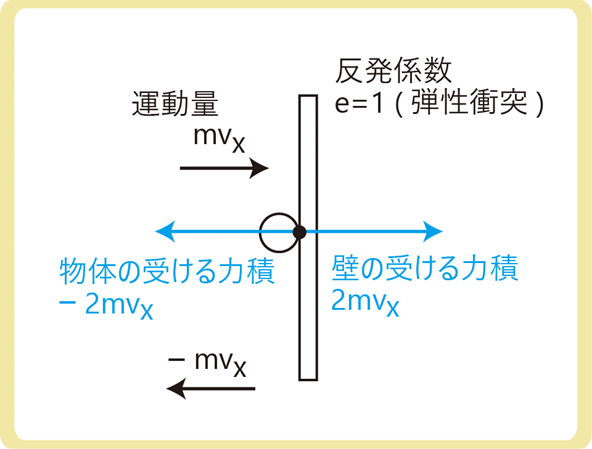
分子が壁に弾性衝突すると、1回につき2mvxの大きさの力積を受けます。
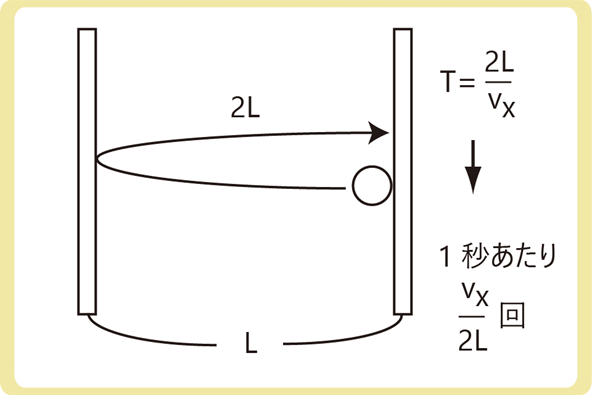
分子が再び同じ壁に衝突するには\(\frac{2L}{v_x}\)秒かかる(距離÷速さ)ので、1秒あたり\(\frac{v_x}{2L}\)回衝突します。
(\(f=\frac{1}{T}\)を用いた。1秒あたりの衝突回数と衝突1回あたりの秒数は逆数の関係)
つまり、1個の分子から受ける1秒あたりの力の大きさは
$$\begin{eqnarray}f&=&2mv_x×\frac{v_x}{2L}\\
&=&\frac{mv_x^2}{L}\end{eqnarray}$$
となり、分子はN個あるため、全ての分子から受ける力は
$$F=\frac{Nm\overline{v_x^2}}{L}$$
となります。
分子1個の速さは\(v\)ですが、全ての分子が同じ速さではありません。
速い分子もあれば遅い分子もあるので、全ての分子の速さを平均して考えます。\(\overline{ }\)(バー)は平均という意味であり、\(\overline{v}\)は平均の速さを表します。
ここで、\(v_x=v_y=v_z\)とすると、\(v^2=v_x^2+ v_y^2+ v_z^2\)より、
$$\begin{eqnarray}v^2&=&v_x^2+ v_y^2+ v_z^2\\
&=&v_x^2+ v_x^2+ v_x^2\\
&=&3v_x^2\\
v_x^2&=&\frac{v^2}{3}\end{eqnarray}$$
となり、これを\(F=\frac{m\overline{v_x^2}}{L}\)に代入すると、
$$F=\frac{Nm\overline{v^2}}{3L}$$
となります。(この先よく出てくる3分の~という形の公式は、\(v^2=3v_x^2\)の3であり、3次元(自由度が3)だからこそ現れる数であると分かりますね。)
圧力は単位面積あたりの力、つまり\(p=\frac{F}{S}\)なので、先ほど求めた力を面積で割ると圧力になります。
$$\begin{eqnarray}p&=&\frac{F}{S}\\
&=&\frac{Nm\overline{v^2}}{3L}×\frac{1}{L^2}\\
&=&\frac{Nm\overline{v^2}}{3L^3}\\
&=&\frac{Nm\overline{v^2}}{3V}\\
pV&=&\frac{Nm\overline{v^2}}{3}\end{eqnarray}$$
となります。理想気体の状態方程式\(pV=nRT\)より、
$$\begin{eqnarray}pV&=&\frac{Nm\overline{v}^2}{3}\\
nRT&=&\frac{Nm\overline{v}^2}{3}\end{eqnarray}$$
となり、これを無理やり、運動エネルギー\(\frac{1}{2}m\overline{v^2}\)の形にすると(両辺に\(\frac{3}{2N}\)をかけると)、
$$\frac{3}{2}\frac{n}{N}RT=\frac{1}{2}m\overline{v^2}$$
となります。
さらに、ここでアボガドロ定数をNAとします。アボガドロ定数は1molあたりの個数、つまり\(\frac{N}{n}\)であるため、
$$\frac{3}{2}\frac{R}{N_A}T=\frac{1}{2}m\overline{v^2}$$
となります。気体定数Rとアボガドロ定数NAはどちらも定数なので、\(\frac{R}{N_A}\)も定数となり。
$$\frac{3}{2}kT=\frac{1}{2}m\overline{v^2}$$
とします。kはボルツマン定数といい、\(\frac{R}{N_A}=k\)です。
気体分子運動論の結論
気体の運動エネルギーは絶対温度に比例する
$$\frac{1}{2}m\overline{v^2}=\frac{3}{2}kT$$
気体分子運動論、\(\frac{3}{2}kT=\frac{1}{2}m\overline{v^2}\)から分かる結論は、気体の運動エネルギーは絶対温度に比例するということです。
物理基礎では、熱運動として分子の運動の激しさを数値で表したものが温度であると勉強しました。
\(\frac{3}{2}kT=\frac{1}{2}m\overline{v^2}\)を見ると、気体分子の運動エネルギーは絶対温度のみで決まるということが分かると思います。
球形容器の場合の気体分子運動論
気体分子運動論の問題は数パターンしかありません。
1つ目は、上で説明したような立方体から考えるパターン
2つ目は、立方体ではなく球形の容器を考えるパターン
3つ目は、立方体や球形容器の壁が動くパターン
です。
ここでは、基本問題としてよく出題される、球形容器の場合における気体分子運動論を解説します。
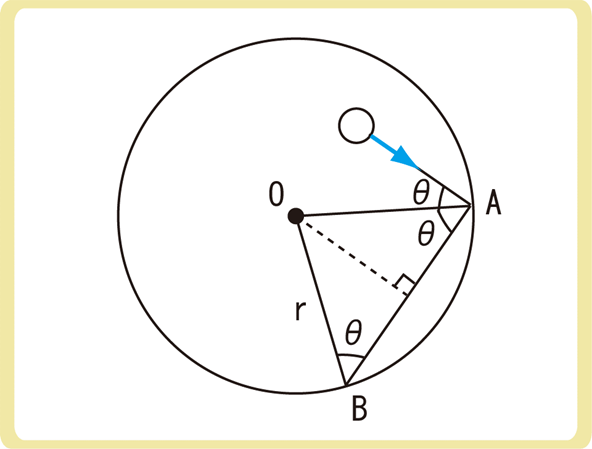
半径がrの球形容器(体積\(V=\frac{4}{3}πr^3\))の中に、速さが\(v\)、質量mの単原子分子がN個あるとします。
立方体で考えたときはxyzの3方向に分けましたが、球形容器は球対称(回転させても同じ形)なので速度を分解しません。
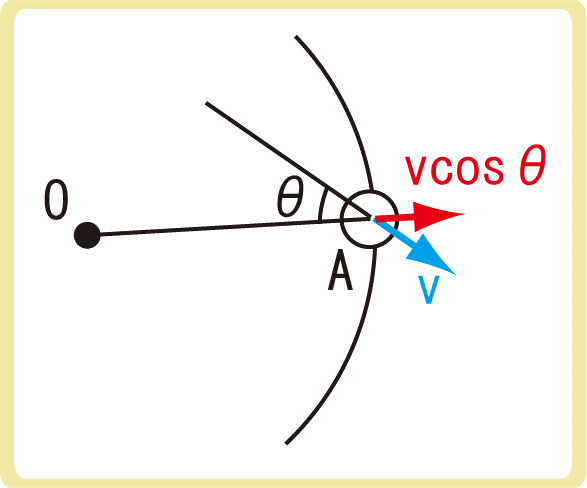
分子が壁に弾性衝突するとき、壁に対して垂直な成分のみ力積を与えるため、1回につき2mvcosθの力積を受けます。
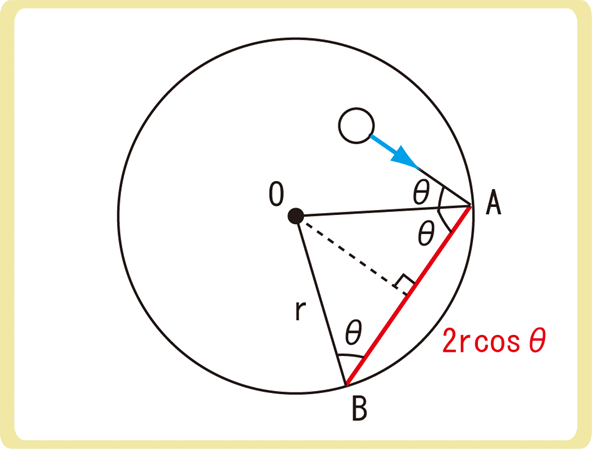
分子が再び壁に衝突するためには、\(\frac{2rcosθ}{v}\)秒かかるため、1秒あたり\(\frac{v}{2rcosθ}\)回衝突します。
(立方体のときは面積をL2とするため同じ壁に限定していましたが、球体の面積を\(4πr^2\)とすれば、同じ場所に当たる必要はなくなる)
つまり、1個の分子から受ける1秒あたりの力の大きさは
$$\begin{eqnarray}f&=&2mvcosθ×\frac{v}{2rcosθ}\\
&=&\frac{mv^2}{r}\end{eqnarray}$$
となります。分子はN個あるため、全ての分子から受ける力は
$$F=\frac{Nm\overline{v}^2}{r}$$
となります。今回は速度を分解していないため、vはそのまま使います。
ここで、圧力は単位面積あたりの力、つまり\(p=\frac{F}{S}\)なので、力を面積で割ると、
$$\begin{eqnarray}p&=&\frac{F}{S}\\
&=&\frac{Nm\overline{v^2}}{r}×\frac{1}{4πr^2}\\
&=&\frac{Nm\overline{v^2}}{4πr^3}\\
&=&\frac{Nm\overline{v^2}}{4πr^3}×\frac{3}{3}\\
&=&\frac{Nm\overline{v^2}}{3}×\frac{3}{4πr^3}\\
&=&\frac{Nm\overline{v^2}}{3}×\frac{1}{V}\\
&=&\frac{Nm\overline{v^2}}{3V}\\
pV&=&\frac{Nm\overline{v^2}}{3}\end{eqnarray}$$
となります。(球の体積は\(V=\frac{4}{3}πr^3\)を利用)
この式は、立方体のときと同じ式であるため、理想気体の状態方程式\(pV=nRT\)を使うところからは同じように式変形して終わりです。
・壁に対して垂直な力積を考える
・面積は\(4πr^2\)なので、力を\(4πr^2\)で割る
・球の体積\(\frac{4}{3}πr^3\)を無理矢理作ってVに変える
これらを使うことで、球の場合の気体分子運動論を解くことができます。
まとめ
気体分子運動論は、気体の分子の運動から、分子の運動エネルギーは絶対温度に比例するということを求める理論のことです。なお、この気体は単原子分子理想気体であることが後々重要になってきます。
立方体の場合と球形容器の場合が頻出のパターンなので、流れを理解できると良いでしょう。












