・平面の合成速度
・平面の相対速度
合成速度と相対速度については物理基礎でも勉強しました。
直線の合成速度と相対速度については、以下の記事を読んでください。
合成速度と相対速度は物理基礎でも勉強しましたが、物理では平面の運動として合成速度と相対速度について勉強します。
物理基礎でも「発展」として扱うことが多いので、物理基礎で勉強している人も多いかもしれませんね。
今回は、平面の運動での合成速度と相対速度について、わかりやすく簡単に解説していきます。
合成速度とは
速度を合成したもの。
\(\vec{v}=\vec{v}_1+\vec{v}_2\)
エスカレーターの上を歩くと、普通に歩くよりも早く動くことができます。
このように、何かの上で移動するときに速度は合成され、その速度を合成速度といいます。
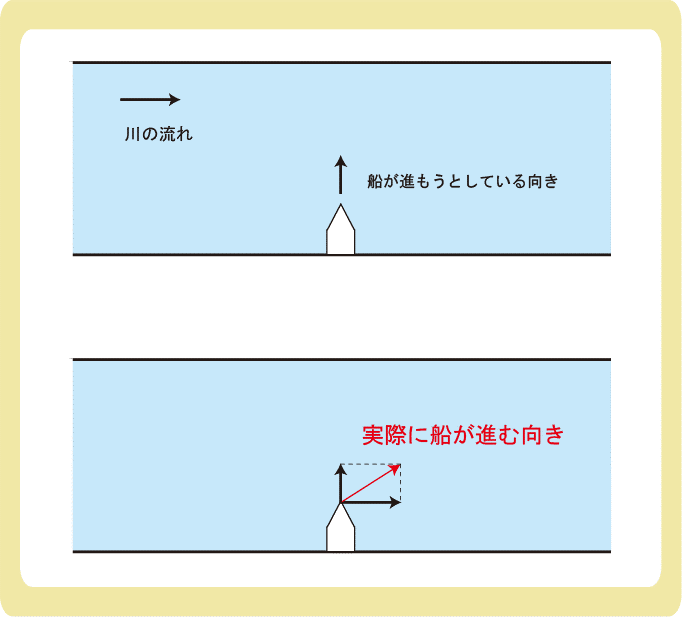
右向きに流れる川を、船がまっすぐ上に進む場合を考えます。
船はまっすぐ上に進もうとするのですが、川が右向きに流れているので、船は右上の方向に進むことになります。
このように、一直線上でなくても、速度を合成することができるのです。
\(\vec{v}=\vec{v}_1+\vec{v}_2\)
速度の合成の公式はベクトルの足し算なので、合成速度の向きや大きさを求めるためには、三平方の定理を使ったり作図をしたりします。
例題
例題1
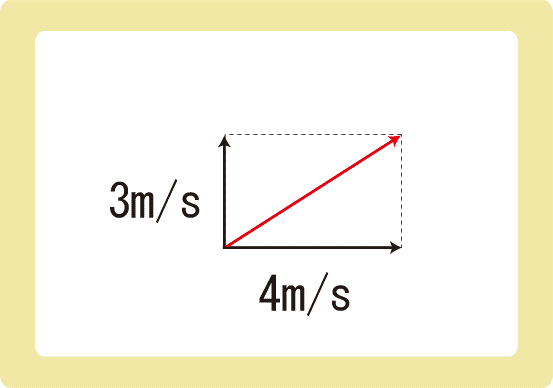
下図のように、4m/sで流れる川幅が30mの川の岸から、静水での速さが3m/sの船が流れと垂直の向きに移動し始めた。以下の各問に答えなさい。
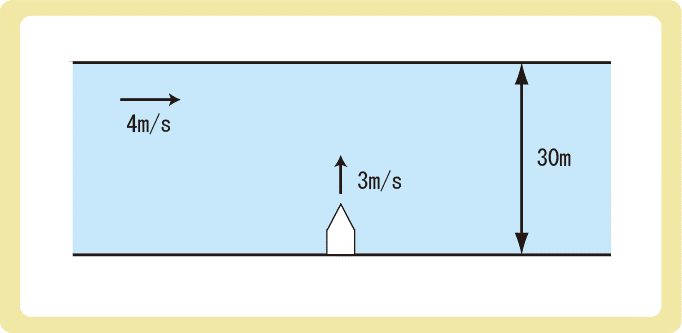
(1)川岸から見た船の速さは何m/sか。
(2)船が川を渡るのに何秒かかるか。
速度の合成は、ベクトルの合成を考えます。
(1)
斜め右上に進む船の速さを求めるためには、三平方の定理を使います。
$$v^2=3^2+4^2\\
v=5$$
∴5m/s
なお、速さはスカラー、速度はベクトルであるため、速さを聞かれた場合、向きを答える必要はありません。
(2)船が斜めに進んでいますが、上向きに3m/sで進みながら右向きに4m/sで進んでいると考えることもできます。
川を渡るためには、上向きの速さだけを考えればよいので、単純に、30mの川を3m/sで進んでいると考えます。
$$30=3×t\\
t=10$$
∴10秒
相対速度とは
ある観測者から見たときの速度。
\(\vec{v}_{AB}=\vec{v}_B-\vec{v}_A\)
相対速度とは、ある観測者から見たときの速度のことをいいます。
Aから見たBの速度のことを、Aに対するBの相対速度といい、
\(\vec{v}_{AB}=\vec{v}_B-\vec{v}_A\)
という式で表します。
必ず、見られている物体の速度－観測者の速度、としなければなりません。
また、ベクトルの引き算なので、相対速度を考えるときは必ず作図しましょう。
例題
例題2
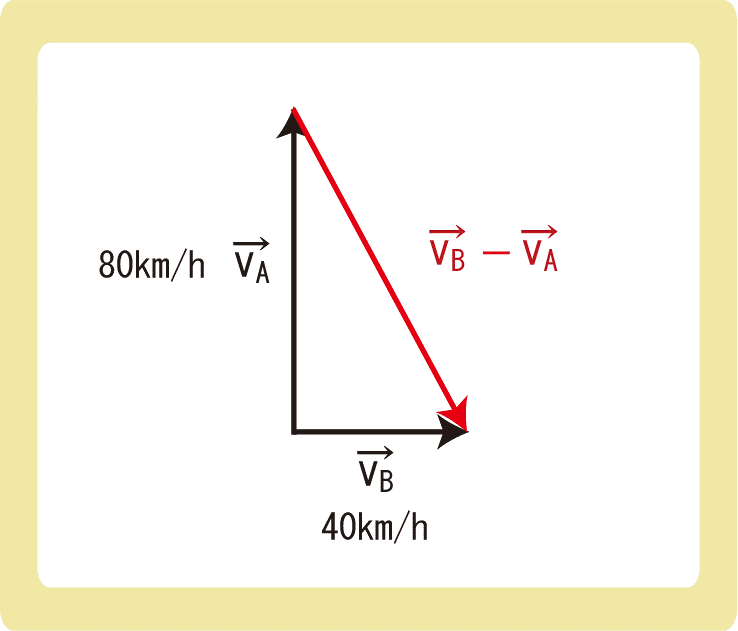
下図のように、xy軸上をA、Bの2つの物体が運動している。Aに対するBの相対速度を求めよ。
相対速度を考えるときは\(\vec{v}_{AB}=\vec{v}_B-\vec{v}_A\)を使います。
直線の場合は速度の大きさをそのまま引いても大丈夫なのですが、平面の運動の場合は、きちんと作図をして、ベクトルの引き算をしなければなりません。
ベクトルの大きさを求める方法は問題によって様々ですが、三平方の定理を使うかsin, cosを使うかのどちらかである場合が大半です。
今回は、三平方の定理を使い、速度の大きさを求めます。
$$v_{AB}=80^2+40^2\\
v_{AB}=40\sqrt{5}$$
∴上図の向きに \(40\sqrt{5}\) m/s
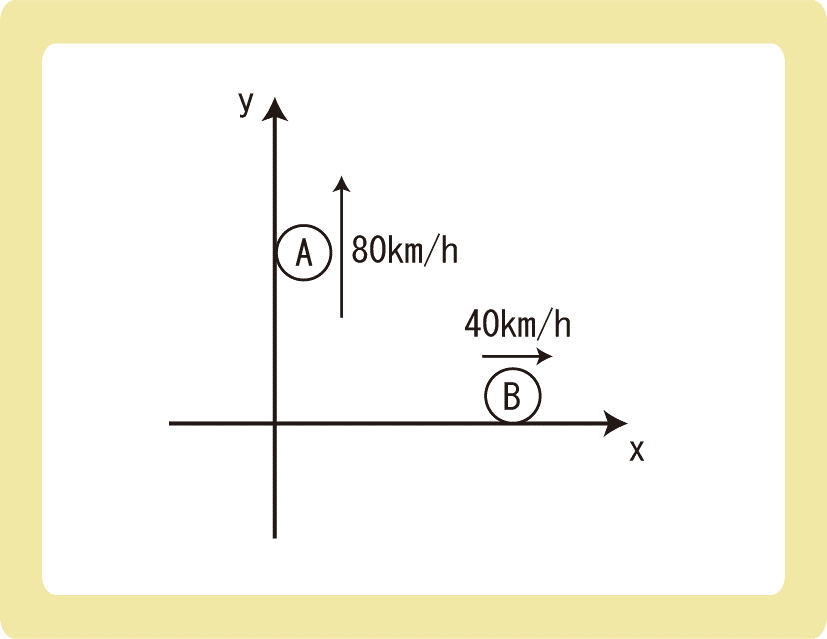
例題3
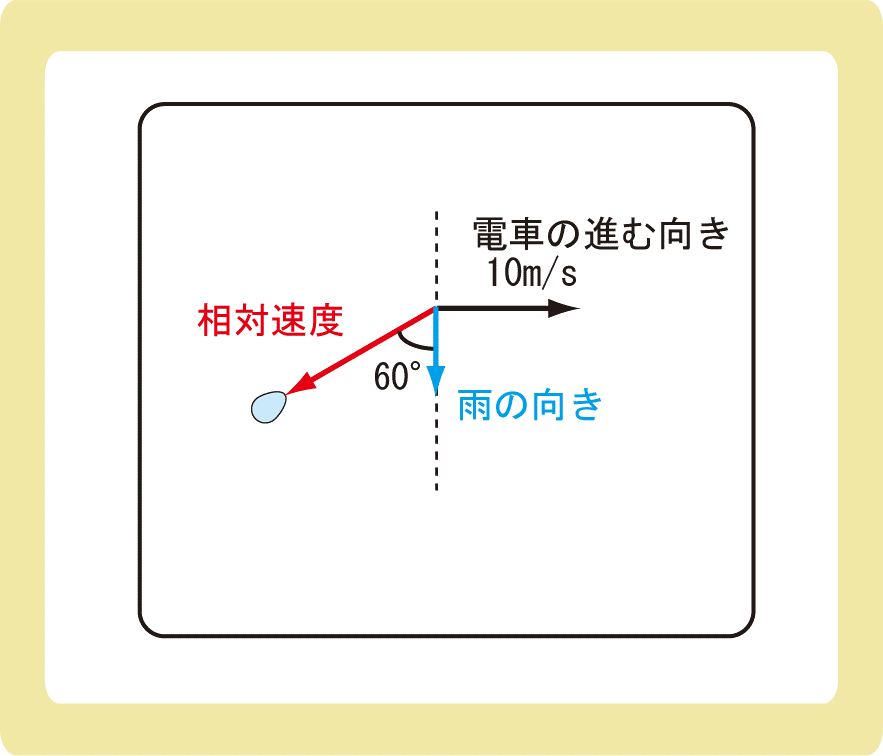
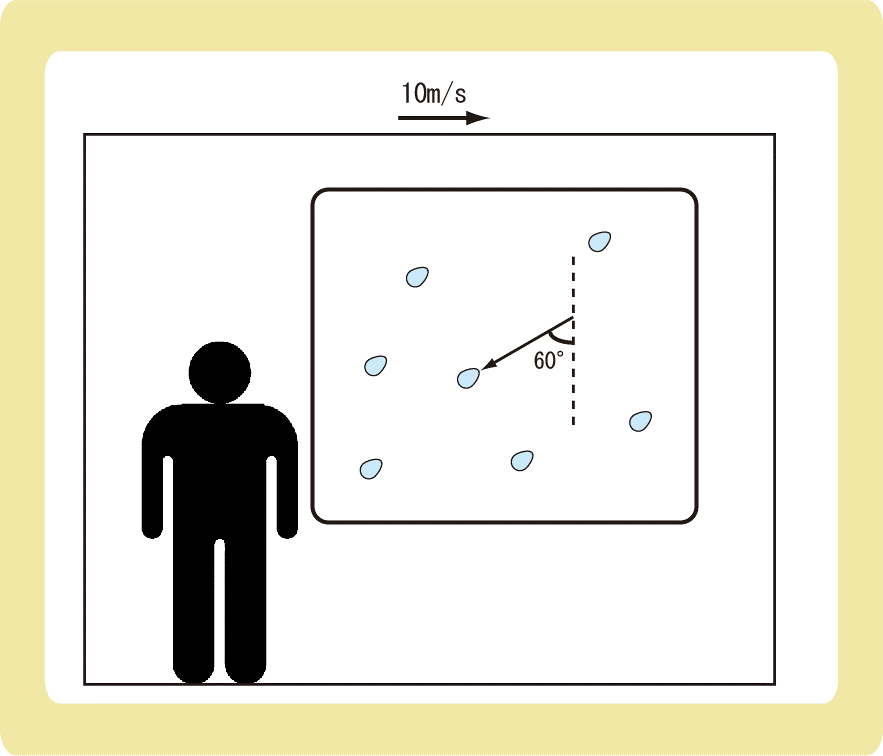
下図のように、垂直に降る雨を10m/sでまっすぐ進む電車の中で見たところ、雨は鉛直方向に対して60°の角をなして降っているように見えた。地面から見た雨の落ちる速さは何m/sか。
雨は垂直に降っているはずなのですが、電車が前に進んでいるせいで、雨が斜め後ろ向きに降っているように見えています。
この3つの矢印の関係から、雨の速さを求めることができます。
なお、上図より、電車の進む向きから雨の向きを見ると、赤色の矢印が相対速度です。
60°の三角形を考えればいいので、雨の速さ\(v\)は
$$v=10×\frac{1}{\sqrt{3}}\\
v=\frac{10\sqrt{3}}{3}$$
となります。
∴\(\frac{10\sqrt{3}}{3}\) m/s
本当は、\(\sqrt{3}\)を1.73にして、有効数字を2桁して答えを求めますが、このサイトでは平方根をそのままにします。ご了承ください。
まとめ
平面の運動での合成速度と相対速度では、ベクトルの足し算や引き算を行います。
川や船など、何かの上を物体が動いているときは合成速度
動いている観測者が何かを見たときの速度は相対速度
として考えましょう。
ベクトルの計算は基本的な計算なので、そこまで難しくはないでしょう。
ベクトルの大きさを求めるときは、三平方の定理か三角比を使うことが非常に多いです。
