ボイル・シャルルの法則とは

今回から、新しく熱力学の範囲を勉強していきます。
力学では物体の運動を中心に勉強しましたが、熱力学では気体の運動について勉強します。

まずは、熱力学の基礎として、圧力・体積・温度の関係を表すボイル・シャルルの法則についてわかりやすく簡単に解説していきます。

熱力学の基本

力学では物体の動きに注目し、質量や重力、速さ等がよく出てきましたが、熱力学では気体の動きに注目するため、圧力p[Pa]、体積V[m³]、絶対温度[K]をよく使います。

絶対温度とは、-273℃を0Kとしたときの温度のことでしたね。もし絶対温度が何か分からない場合は、物理基礎の復習からしてください。

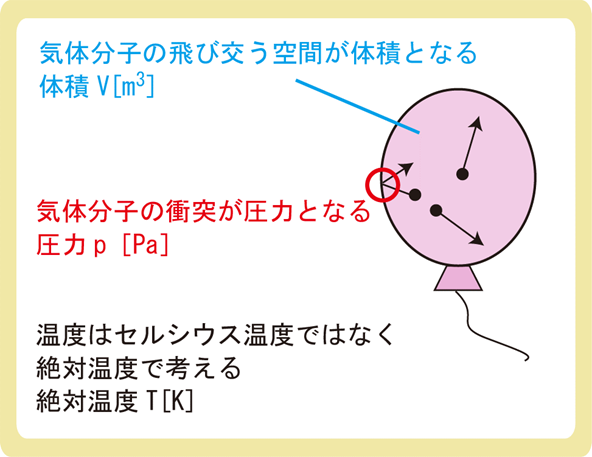
上図のように、風船の中に気体が入っている状態を考えましょう。

風船の中の気体は不規則に運動しており、風船に衝突しています。気体分子1つ1つの影響は小さいのですが、大量の分子が衝突することによって無視できない大きさの圧力が生じます。

風船や気球、容器の中など、気体分子の飛び交う空間を体積Vで表し、温度はセルシウス温度ではなく絶対温度Tを使います。

ボイルの法則とは

ボイルの法則とは、気体の温度・質量が一定のとき、気体の体積と圧力は反比例する法則のことです。

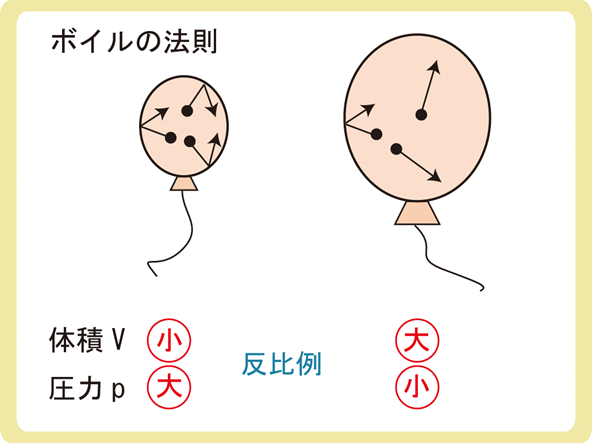
上図がボイルの法則のイメージです。

体積が小さいと、気体の分子が衝突する回数が増えるため圧力が大きくなります。体積が大きい場合はその逆ですね。

体積Vを\(\frac{1}{2}\)倍にすると圧力Pが2倍、体積Vを\(\frac{1}{3}\)倍にすると圧力Pが3倍、つまり、体積と圧力は反比例します。式でいうと\(pV=一定\)です。

シャルルの法則とは

シャルルの法則とは、気体の圧力・質量が一定のとき、気体の体積と絶対温度は比例する法則のことです。

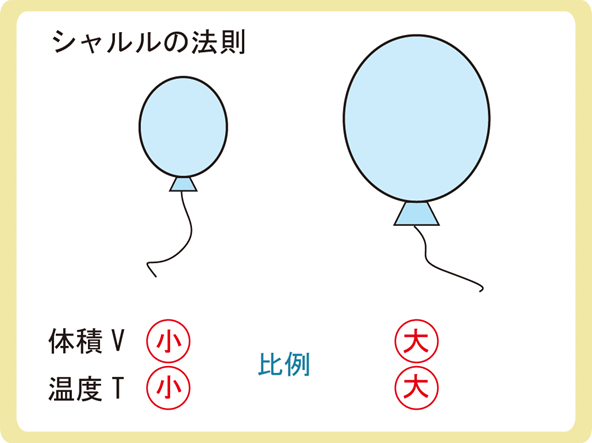
気球をイメージすると分かりやすいかもしれません。
気体を温めると気体の体積は大きくなり、気体の温度が下がると気体の体積も小さくなります。

絶対温度Tが2倍になると体積Vも2倍に、絶対温度Tが3倍になると体積Vも3倍に、つまり、絶対温度Tと体積Vは比例関係にあるのです。式でいうと\(\frac{V}{T}=一定\)です。

なお、セルシウス温度を2倍にしても体積は2倍になりません。きちんと絶対温度で考えましょう。

ボイル・シャルルの法則とは

ボイル・シャルルの法則とは、気体の質量が一定のとき、気体の体積は圧力に反比例し、絶対温度に比例する法則のことつまり、ボイルの法則とシャルルの法則を合わせて考えた法則のことです。

\(\frac{V}{T}=一定\)と\(pV=一定\)を合わせると\(\frac{pV}{T}=一定\)となります。

例題

例題1

ある一定の量の気体の圧力を一定にしたまま、体積を2倍にした。この気体の絶対温度は何倍になるか。

例題2

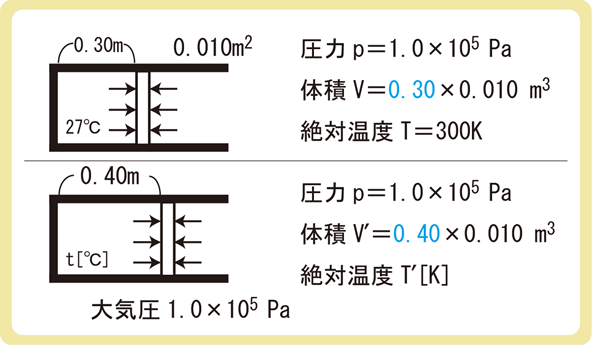
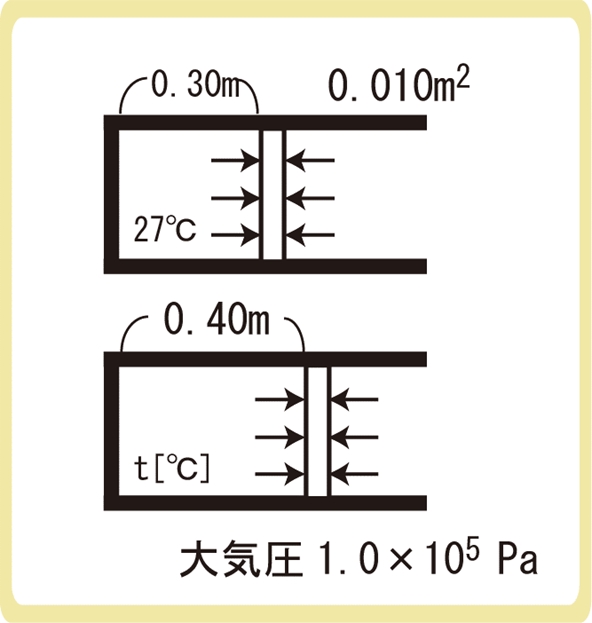
下図のように、断面積0.010m²のなめらかなピストンが付いた容器が水平に置かれている。ピストンによって閉じ込められている空気の温度が27℃であり、ピストンの容器の底から0.30mの位置にあった。この容器を熱し、容器内の気体の温度を上げると、ピストンは容器の底から0.40mの位置で静止した。この気体の温度は何℃か。ただし、大気圧を1.0×10⁵Paとする。

まとめ

ボイルの法則とは、温度が一定のとき、圧力と体積が反比例すること。
シャルルの法則とは、圧力が一定の解き、体積と絶対温度が比例することをいいます。

この2つの法則を組み合わせたものがボイル・シャルルの法則です。
ボイルの法則とシャルルの法則を使う問題は、わざわざ使い分けなくてもボイル・シャルルの法則を使うことで解くことができるのですが、次の内容で勉強する理想気体の状態方程式を使っても解くことができるため、あまり出番はないかもしれません。

次の内容はこちら

一覧に戻る